典拠
ACMが示している、コンピュータ科学の専門教育のカリキュラムガイドライン Curriculum Guidelines for Undergraduate Programs in Computer Science の2013年版(CS2013, https://www.acm.org/education/curricula-recommendations#h-computer-science )で例示されている時間の割り振りと内容を見るとそうなっている。
詳しく
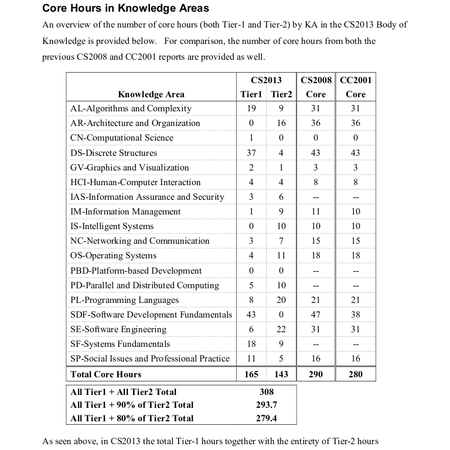
CS2013 では、次のように基本的な内容を Tier-1、発展的な内容を Tier-2 として時間の割り振りの例を示しているが(p. 37)、
まず Software Development Fundamentals(SDF)に、次いで Discrete Structures(DS)に、多大な時間を割り振っていることがわかる。そして、それぞれの説明には次のようにある。
SDF
(p. 167) Fluency in the process of software development is a prerequisite to the study of most of computer science. In order to use computers to solve problems effectively, students must be competent at reading and writing programs in multiple programming languages. Beyond programming skills, however, they must be able to design and analyze algorithms, select appropriate paradigms, and utilize modern development and testing tools. ...
コンピュータ科学で何をやるにもほぼプログラミングは大前提であり、複数のプログラミング言語を読み、書けなければならない、といったようにある通り、プログラミング抜きにはコンピュータ科学はありえない、という考えかたが背後にあることがよくわかると思う。またそれに続けて、アルゴリズムの設計や分析、といったように書かれているように、プログラミングとは単にコードを書くことではなく、アルゴリズムなどについても当然含まれる、といった考えかたであることもわかる。
DS
(p. 76) Discrete structures are foundational material for computer science. By foundational we mean that relatively few computer scientists will be working primarily on discrete structures, but that many other areas of computer science require the ability to work with concepts from discrete structures. Discrete structures include important material from such areas as set theory, logic, graph theory, and probability theory.
The material in discrete structures is pervasive in the areas of data structures and algorithms but appears elsewhere in computer science as well. For example, an ability to create and understand a proof—either a formal symbolic proof or a less formal but still mathematically rigorous argument—is important in virtually every area of computer science, including (to name just a few) formal specification, verification, databases, and cryptography. Graph theory concepts are used in networks, operating systems, and compilers. Set theory concepts are used in software engineering and in databases. Probability theory is used in intelligent systems, networking, and a number of computing applications.
「離散構造」などと訳されることもあり、また数学の分野としては離散数学などと呼ばれることもあるが、そのあたりの分野である。大学などでは、これらの授業で習った内容について、すぐに(忘れないうちに)応用したプログラムを提出させている所などもあると思うが、プログラミングと密接している最重要分野といってよい。